Low Density Parity Check Code

Abstract
This page summarizes some contributions in the field of architecture of LDPC decoder. Those contributions correspond mainly to:
- Early work (1998, during my sabbatical stay in University of Toronto): definition of a code construction hardware friendly.
- PhD of Frederic Guilloud (2001-2004): sub-optimal check node processing, generic architecture of decoder
- PhD of Cedric Marchand (2007-2010): Optimisation of DVB-S2 decoder (precision, scheduling, solution to solve problem of double diagonals of the parity check matrix).
- Sabbatical stay in Lab-STICC of Chris Winstead (2013-2014): Low complexity LDPC decoder (one bit per message).
- New construction of QC-LDPC matrices with high girth (2018-19).
- Noise Against Noise LDPC decoder (2016-19): go to the ANR NAND Project WEB site.
- General articles on LDPC architecture.
With the sabbatical stay of Chris Winstead in my lab in 2013/2014, I also start to work on bit-flipping algorithm.
On this topic, you can see the presentation of Chris Winstead and the papers related to this topic.

Early work (1998-1999)
During my sabbatical year in Toronto in 1998, I proposed with F. Kschischang to constraint the parity check matrix in order to solve a priori all memory conflicts for a parallel architecture of a LPDC decoder.
This work lead to a single seminal paper in 2000:
- Emmanuel Boutillon, Jeff Castura, Frank R. Kschischang, "Decoder-First Code Design", Proceedings of the 2nd International Symposium on Turbo
Codes and Related Topics, pp 459-462, Brest, France, Sept. 2000.

PhD of Frederic Guilloud (2001-2004)
In the frame of the PhD of Frederic Guilloud, "Architecture générique de décodeur de codes LDPC" (PhD report (2.6 Mo)), two contributions have been proposed. The first one is the proposition of a new algorithm, named
lambda-Min algorithm, for updating extrinsic information. The lambda-Min algorithm offers different trade-off performance versus complexity between the belief propagation (BP) algorithm (optimal but complex) and the
universal most powerful (UMP) BP-based algorithm (simple but leading to significant performance degradation in some cases). Hardware implementation of the lambda-Min algorithm in a serial mode is also discussed. Reduction up to 75 pourcent without any significant degradation of the performance. The second contribution is the formal classification of LDPC decoder architecture.
Related publications
- F. Guilloud, E. Boutillon, J. Tousch, J.L. Danger,
"Generic description and synthesis of LDPC decoder", IEEE Transactions On Communications, IEEE Transactions on
Communications, Vol. 55, n°11, pp 2084 - 2091, nov. 2007.
- Fédéric Guilloud, Emmanuel Boutillon, Jacky Tousch,
"Description et synthèse générique des décodeurs de codes LDPC", Journées Francophones sur l’Adéquation Algorithme Architecture, Dijon, Janv. 2005.
- Frédéric Guilloud, "Generic
Architecture for LDPC Codes Decoding", PHD Thesis, ENST Paris, July the 2nd, 2004. (slides of the
presentation: slides)
- Jacky Tousch, Emmnuel Boutillon, David Gnaedig, "appareil de décodage de code LDPC",
French Patent pending, june 19, 2004.
- E. Boutillon, J. Tousch, F. Guilloud, "LDPC decoder, corresponding method, system and computer programm", United States Patent n°7174495, Feb. 6, 2007 (deposal n°10/742,643, dec. 19, 2003).
- Frédéric Guilloud, Emmanuel Boutillon, Jean-Luc Danger, ""lambda-Min
Decoding Algorithm of Regular and Irregular LDPC Codes"", 3nd International Symposium on Turbo Codes and Related Topics, Brest, France, pp
451-454, Sept. 2003, (Poster of the paper).
- F. Guilloud, E. Boutillon, J.-L. Danger, "Décodage
des codes LDPC par l'algorithme lambda-Min", GRETSI 2003, Paris, Sept. 2003, (Poster of the paper).
Miscellaneous
- Organization of a one day workwhop on LDPC (Paris, december 19, 2002): Journée LDPC GDR-ISIS (in french).
- Slides of the talk given at University of Massachusset, University of
Toronto, University of Minneapolis, University of Alberta (feb-march 2003): slides.
- "Architecture de décodeur LDPC", SCEE seminar,
SUPELEC, Rennes, april 7th, 2005 : slides (in french).
- Slides of the talk given by Frederic Guilloud at 2005 IEEE Communication Theory Workshop (Utah, june 2005)
: slides.
- "Proposition d'une méthodologie d'adéquation algorithme architecture", E. Boutillon, GDR-ISIS meeting (Paris, 27/06/2005): slides (pdf) and
slides (powerpoint).
- "Architecture générique de décodage de code LDPC", E. Boutillon, CNES meeting (Toulouse, 29/06/2006): slides (pdf)
- "Generic model of LDPC code decoders", E. Boutillon, NewCom meeting (Pisa, 6/10/2006): slides (pdf)

PhD of Cedric Marchand (2007-2010)
This thesis was funded by NXP. It was dedicated to the hardware implementation of the LDPC decoder of the DVB-S2, -T2 and C2 standard s(Digital Video Broadcasting by Satellite, Terrestrial and Cable). The layered decoder is chosen as the basis architecture for the decoder implementation. We had to deal with the memory conflicts due to the matrix structure specific to the DVB-S2, -T2, -C2 standards. Two new contributions have been studied to solve the problem. The first is based on the construction of an equivalent matrix and the other relies on the repetition of layers. The conflicts inherent to the pipelined architecture are solved by an efficient scheduling found with the help of graph theories.
Memory size is a major point in term of area and consumption, therefore the reduction to a minimum of this memory is studied. A well defined saturation and an optimum partitioning of memory bank lead to a significant reduction compared to the state-of-the-art. Moreover, the use of single port RAM instead of dual port RAM is studied to reduce memory cost.
Related Publications
- C. Marchand; Laura Conde-Canencia; Emmanuel Boutillon
High-speed conflict-free layered LDPC decoder for the DVB-S2, -T2 AND -C2 standards
2013 IEEE Workshop on Signal Processing Systems (SISP'2013), Tapei, pp. 1-6, Oct 2013.
- C. Marchand, L. Conde-Canencia, E. Boutillon, " Architecture and finite precision optimization for layered LDPC Decoders
", Journal of Signal Processing Systems, Springer, pp. 185-197, vol. 65, n°2, Nov. 2011.
- C. Marchand, L. Conde-Canencia, E. Boutillon, "Architecture and finite precision optimization for layered LDPC decoders",
Processing Systems (SIPS’2010), San Franscisco, Oct 2010.
- C. Marchand, J.-B. Doré, L. Conde-Canencia, E. Boutillon, "Conflict Resolution by Matrix Reordering for DVB-T2 LDPC
Decoders", Globecom 2009, Haiwai, Dec. 2009.
- C. Marchand, J.-B. Doré, L. Conde-Canencia, E. Boutillon,"Conflict resolution for pipelined layered LDPC decoders", SIPS 2009, Tampere, Oct. 2009.
Note: [2] is an extended version of [3] published after the SISP'2010 conference.

PhD of Yangyang Tang (2010-2013)
This thesis addresses the issue of designing on unreliable circuit. One of the solution explored during the PhD uses LDPC decoder to correct internal upset errors. Since the LDPC decoder is itself embedded in the noisy architecture, it is also subject to internal errors. New LDPC architecture (based on the C-Muller gate) is proposed to perform a robust variable node architecture.
Related publications
- Yangyang Tang (january 2013), "Computation on Unreliable Architecture"(PhD report (6.5 Mo))
- C. Winstead, Y. Tang,, E. Boutillon, C. Jego, Christophe and M. Jézéquel, A Space-Time Redundancy Technique for Embedded Stochastic Error Correction, 7th International Symposium on Turbo Codes & Iterative Information Processing, Gothenburg, Sweden, august 2012.
- Y. Tang, C. Winstead, E. Boutillon, C. Jego, Christophe and M. Jézéquel, An LDPC decoding method for fault-tolerant digital logic, IEEE International Symposium on Circuits and Systems (ISCAS), pp: 3025-3028, Seoul, may 2012.

Sabbatical of Chris Winstead (2013-2014) in Lab-STICC
Chris Winstead spent a sabbatical year (funded by a Fulbright grant) from June 2013 to May 2014 in Lab-STICC. During this period, we have collaborated on low complexity LDPC decoder based on bit-flipping algorithm.
Related Publications
- C. Winstead, E. Boutillon, "Decoding LDPC Codes with Locally Maximum-Likelihood Binary Messages", IEEE Communications Letters, Accepted for publications, available on line., pp.4
- G. Sundararajan, C. Winstead, E. Boutillon, Noisy Gradient Descent Bit-Flip Decoding for LDPC Codes, IEEE Transactions on Communications, 62 (10), pp.16 Octobre. 2014.
- C. Winstead; G. Sundararajan; E. Boutillon, "A Case Study in Noise Enhanced Computing: Noisy Gradient Descent Bit Flip Decoding., Designing with Uncertainty - Opportunities & Challenges workshop, Mar 2014, United Kingdom.
Miscellaneous
- Slides of the presentation given by Chris Winstead in Telecom Bretagne the 22nd of April 2014:
Recent results on Bit Flipping LDPC decoders
- Slides of the presentation given by Emmanuel Boutillon the 4th November 2014 (GDR SoCSiP-ISIS) day on Error Control Code architecture
A Survey On Binary Message LDPC Decoder
- WEB site of Chris Winstead'Lab: Low-Energy / Fault-Tolerant systems laboratory

New construction of QC-LDPC matrices with high girth (2018-19).
In the last section of [1]), N); N = we presented a new method to generates QC-LDPC with high girth. For a complete prototype matrix of size (J=3,L), we give the minimum expansion factor required
to obtain a girth 10 expanded matrix. The first colunm of the table gives the values of L, the second colunm report the values of expansion factor P found in [1]), N); N = the third colunm gives
the value of L proposed in [2]), N); N = the fourth column presents the smaller P values found since the publication while the fifth column gives a lower bound developped in [3].
[1]Alban Derrien, Emmanuel Boutillon, Audrey Cerqueus. Additive, Structural and Multiplicative Transformations for the Construction of Quasi-Cyclic LDPC matrices.
IEEE Transactions on Communications, doi: 10.1109/TCOMM.2018.2890251, in press, 2019 ( available online).
[2]M. Battaglioni, A. Tasdighi, M. Baldi, M. H. Tadayon and F. Chiaraluce, "Compact QC-LDPC Block and SC-LDPC Convolutional Codes for Low-Latency Communications," 2018 IEEE 29th
Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Bologna, 2018, pp. 1-5.
[3] M. Karimi and A.H. Banihashemi. "On the girth of quasi-cyclic protograph LDPC codes". IEEE Trans. Inf Theory, vo1.S9, no.7, pp.4542-45S2, July 2013.
Table I: Minimum expansion factor found to obtain a girth 10 QC-LDPC matrix from (J=3, L) complete prototype matrix
| Value of L | Value of P [1] | Value of P [2] | New found P | Low bound [3] | (m,n) matrix size | (k,n) LDPC code | code rate |
| L = 4 | 37 | 37 | 37 | 37 | (111, 148) | (37, 148) | 0.250 |
|---|
| L = 5 | 61 | 61 | 61 | 61 | (183, 305) | (122, 305) | 0.400 |
|---|
| L = 6 | 91 | 91 | 91 | 91 | (273, 546) | (273, 546) | 0.500 |
|---|
| L = 7 | 139 | 137 | 129 | 127 | (387, 903) | (516, 903) | 0.571 |
|---|
| L = 8 | 201 | 181 | 181 | 169 | (543, 1448) | (905, 1448) | 0.625 |
|---|
| L = 9 | 280 | 241 | 219 | 217 | (657, 1971) | (1314, 1971) | 0.667 |
|---|
| L = 10 | 383 | 313 | 273 | 271 | (819, 2730) | (1911, 2730) | 0.700 |
|---|
| L = 11 | 507 | 397 | 373 | 331 | (1119, 4103) | (2984, 4103) | 0.727 |
|---|
| L = 12 | - | 523 | 463 | 397 | (1389, 5556) | (4167, 5556) | 0.750 |
|---|
| L = 13 | - | - | 571 | 469 | (1713, 7423) | (5710, 7423) | 0.769 |
|---|
| L = 14 | - | - | 687 | 547 | (2061, 9618) | (7557, 9618) | 0.786 |
|---|
| L = 15 | - | - | 823 | 631 | (2469, 12345) | (9876, 12345) | 0.800 |
|---|
| L = 16 | - | - | 1009 | 721 | (3027, 16144) | (13117, 16144) | 0.813 |
|---|
| L = 17 | - | - | 1191 | 817 | (3573, 20247) | (16674, 20247) | 0.824 |
|---|
| L = 18 | - | - | 1399 | 919 | (4197, 25182) | (20985, 25182) | 0.833 |
|---|
| L = 19 | - | - | 1657 | 1027 | (4971, 31483) | (26512, 31483) | 0.842 |
|---|
| L = 20 | - | - | 1929 | 1141 | (5787, 38580) | (32793, 38580) | 0.850 |
|---|
| L = 21 | - | - | 2203 | 1261 | (6609, 46263) | (39654, 46263) | 0.857 |
|---|
| L = 22 | - | - | 2473 | 1387 | (7419, 54406) | (46987, 54406) | 0.864 |
|---|
| L = 23 | - | - | 2797 | 1519 | (8391, 64331) | (55940, 64331) | 0.870 |
|---|
| L = 24 | - | - | 3181 | 1657 | (9543, 76344) | (66801, 76344) | 0.875 |
|---|
| L = 25 | - | - | 3583 | 1801 | (10749, 89575) | (78826, 89575) | 0.880 |
|---|
| L = 26 | - | - | 3919 | 1951 | (11757, 101894) | (90137, 101894) | 0.885 |
|---|
| L = 27 | - | - | 4483 | 2107 | (13449, 121041) | (107592, 121041) | 0.889 |
|---|
| L = 28 | - | - | 5119 | 2269 | (15357, 143332) | (127975, 143332) | 0.893 |
|---|
| L = 29 | - | - | 5179 | 2437 | (15537, 150191) | (134654, 150191) | 0.897 |
|---|
| L = 30 | - | - | 6037 | 2611 | (18111, 181110) | (162999, 181110) | 0.900 |
|---|
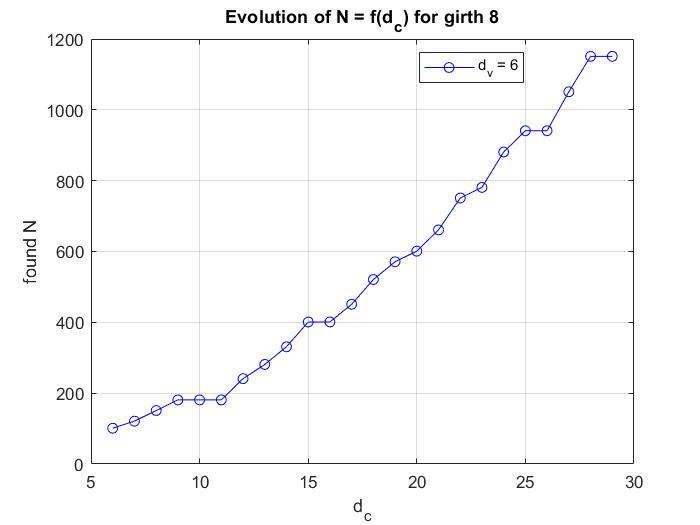
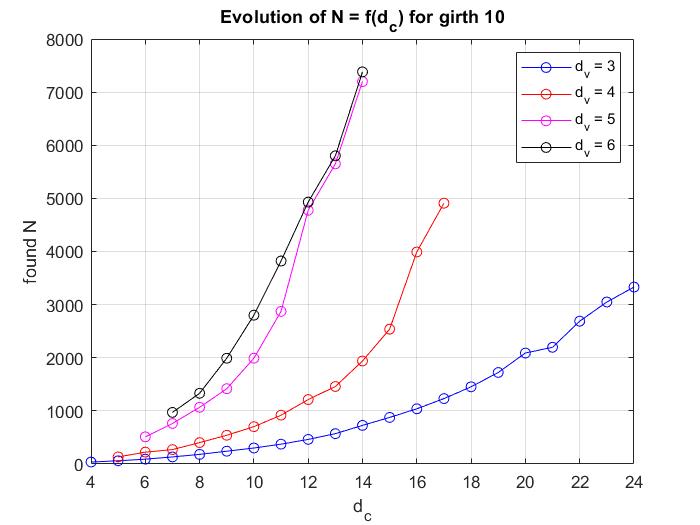
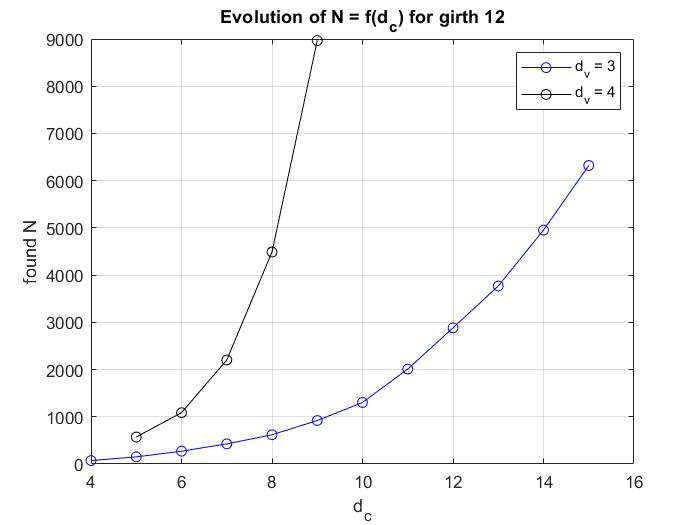
This figure shows the evolution of P as a function of L for L= 4 to 15
.jpg)
If you are interested to know the new matrices, please send a mail to "emmanuel.boutillon@univ-ubs.fr" with the subjet: "request for QC-LDPC matrices". In the core of the mail,
you should indicate the sizes of matrices that you need. If you know other papers or better matrices with smaller expension factors, please, fell free to send an email to inform me.

QC-LDPC matrices with high girth (2020-21).
This section presents the fully connected exponent matrices presented in [1]. Newly found expansion factor will be updated. The matlab commands
to generate the prototype matrix is proposed. A simple matlab code that evaluate the girth of the generated QC-LPDC matrix is given " Here ".
Alireza Tasdighi, Emmanuel Boutillon, "Integer Ring Sieve for Constructing Compact QC-LDPC Codes with Girths 8, 10, and 12.", Submitted to IEEE Trans. on Information Theory, Feb. 2021.
m = 3, girth 10.
N = 37; P = mod( kron([0, 1, 27]', [0, 1, 3, 24]), N);
N = 61; P = mod( kron([0, 1, 14]', [0, 1, 3, 21, 55]), N);
N = 91; P = mod( kron([0, 1, 17]', [0, 1, 3, 7, 25, 38]), N);
N = 133; P = mod( kron([0, 1, 12]', [0, 1, 3, 32, 38, 42, 116]), N);
N = 181; P = mod( kron([0, 1, 133]', [0, 1, 3, 69, 120, 129, 141, 156]), N);
N = 241; P = mod( kron([0, 1, 16]', [0, 1, 3, 13, 88, 114, 182, 217, 223]), N);
N = 301; P = mod( kron([0, 1, 80]', [0, 1, 3, 7, 33, 73, 117, 140, 208, 226]), N);
N = 373; P = mod( kron([0, 1, 285]', [0, 1, 3, 35, 50, 73, 95, 170, 180, 221, 235]), N);
N = 463; P = mod( kron([0, 1, 442]', [0, 1, 3, 9, 29, 116, 148, 219, 260, 329, 388, 418]), N);
N = 571; P = mod( kron([0, 1, 462]', [0, 1, 3, 9, 91, 120, 140, 217, 375, 398, 511, 516, 561]), N);
N = 727; P = mod( kron([0, 1, 446]', [0, 1, 3, 7, 12, 35, 105, 192, 213, 352, 442, 472, 653, 714]), N);
N = 877; P = mod( kron([0, 1, 595]', [0, 1, 3, 7, 12, 22, 47, 114, 247, 390, 423, 431, 639, 692, 755]), N);
N = 1039; P = mod( kron([0, 1, 899]', [0, 1, 3, 7, 12, 20, 36, 183, 396, 462, 674, 716, 798, 823, 967, 982]), N);
N = 1231; P = mod( kron([0, 1, 1105]', [0, 1, 3, 7, 12, 20, 34, 106, 132, 374, 402, 450, 519, 737, 1010, 1061, 1071]), N);
N = 1453; P = mod( kron([0, 1, 760]', [0, 1, 3, 7, 12, 20, 30, 46, 132, 184, 239, 320, 418, 867, 951, 1015, 1100, 1382]), N);
N = 1723; P = mod( kron([0, 1, 1682]', [0, 1, 3, 7, 12, 20, 30, 46, 67, 99, 248, 605, 693, 793, 831, 975, 1105, 1271, 1381]), N);
N = 2089; P = mod( kron([0, 1, 1263]', [0, 1, 3, 7, 12, 20, 30, 45, 61, 85, 107, 249, 510, 602, 970, 1022, 1297, 1481, 1635, 1987]), N);
N = 2197; P = mod( kron([0, 1, 1161]', [0, 1, 125, 122, 251, 1533, 493, 2191, 1416, 867, 2083, 877, 1794, 413, 303, 811, 846, 1262, 1438, 1739, 2109]), N);
N = 2689; P = mod( kron([0, 1, 2298]', [0, 1, 196, 66, 522, 1998, 524, 1109, 1343, 1217, 432, 39, 2255, 1257, 17, 466, 1596, 1788, 2346, 2504, 2524, 2618]), N);
N = 3049; P = mod( kron([0, 1, 2517]', [0, 1, 267, 89, 710, 2145, 726, 2338, 639, 1971, 2886, 2445, 2077, 1424, 1821, 414, 586, 612, 1002, 1373, 1504, 1573, 2646]), N);
N = 3331; P = mod( kron([0, 1, 1868]', [0, 1, 404, 407, 2676, 1209, 399, 557, 1623, 2013, 3231, 1878, 2436, 716, 242, 916, 31, 1843, 1941, 1998, 2229, 2318, 2618, 3139]), N);
N = 3577; P = mod( kron([0, 1, 1452]', [0, 1, 674, 677, 1346, 571, 2700, 7, 3467, 580, 2895, 1657, 2916, 2443, 91, 3204, 1033, 3049, 3523, 164, 1070, 2651, 2772, 2931, 3144]), N);
m = 3, girth 12.
N = 73; P = mod( kron([0, 1, 9]', [0, 1, 3, 13]),N);
N = 151; P = mod( kron([0, 1, 119]', [0, 1, 3, 108, 139]), N);
N = 271; P = mod( kron([0, 1, 29]', [0, 1, 3, 7, 67, 144]), N);
N = 427; P = mod( kron([0, 1, 136]', [0, 1, 3, 18, 209, 300, 388]), N);
N = 619; P = mod( kron([0, 1, 367]', [0, 1, 3, 216, 312, 318, 462, 529]), N);
N = 921; P = mod( kron([0, 1, 632]', [0, 1, 3, 117, 226, 232, 384, 441, 595]), N);
N = 1303; P = mod( kron([0, 1, 1208]', [0, 1, 14, 5, 89, 349, 383, 562, 1130, 1152]), N);
N = 2011; P = mod( kron([0, 1, 1806]', [0, 1, 30, 10, 3, 122,454,654,937,1095,1699]), N);
N = 2883; P = mod( kron([0, 1, 2444]', [0, 1, 522, 442, 965, 11, 902, 1145, 1857, 2091, 2632, 2775]), N);
N = 3769; P = mod( kron([0, 1, 3306]', [0, 1, 154, 1257, 2564, 3099, 1636, 19, 1539, 2519, 2855, 3111, 3250]), N);
N = 4953; P = mod( kron([0, 1, 1544]', [0, 1, 108, 1546, 1331, 4308, 3839, 4746, 2558, 457, 486, 1252, 4262, 4911]), N);
N = 6321; P = mod( kron([0, 1, 2273]', [0, 1, 4380, 4051, 1613, 5328, 827, 3891, 5171, 4342, 1637, 2135, 4082, 4694, 5905]), N);
m = 4, girth 10.
N = 133; P = mod( kron([0, 1, 11, 121]', [0, 1, 5, 21, 54]), N);
N = 223; P = mod( kron([0, 1, 39, 183]', [0, 1, 3, 9, 45, 59]), N);
N = 271; P = mod( kron([0, 1, 28, 242]', [0, 1, 3, 7, 141, 221, 255]), N);
N = 403; P = mod( kron([0, 1, 87, 315]', [0, 1, 3, 7, 111, 159, 233, 303]), N);
N = 541; P = mod( kron([0, 1, 129, 411]', [0, 1, 3, 99, 264, 314, 353, 401, 423]), N);
N = 703; P = mod( kron([0, 1, 26, 676]', [0, 1, 9, 123, 353, 443, 498, 501, 609, 663]), N);
N = 919; P = mod( kron([0, 1, 52, 866]', [0, 1, 3, 158, 113, 349, 509, 677, 702, 725, 772]), N);
N = 1213; P = mod( kron([0, 1, 217, 995]', [0, 1, 3, 653, 1088, 798, 29, 195, 370, 476, 574, 713]), N);
N = 1459; P = mod( kron([0, 1, 339, 1119]', [0, 1, 487, 1313, 1053, 740, 533, 398, 504, 662, 664, 685, 970]), N);
N = 1939; P = mod( kron([0, 1, 1822, 116]', [0, 1, 3, 1590, 1357, 112, 579, 152, 254, 323, 417, 848, 975, 1863]), N);
N = 2539; P = mod( kron([0, 1, 2232, 306]', [0, 1, 3, 920, 1533, 278, 2515, 1504, 333, 538, 317, 404, 769, 1437, 2383]), N);
N = 3991; P = mod( kron([0, 1, 3701, 289]', [0, 1, 3, 869, 1448, 1062, 777, 2220, 3507, 10, 30, 41, 164, 845, 1632, 1808]), N);
N = 4909; P = mod( kron([0, 1, 4335, 573]', [0, 1, 3, 1721, 2868, 467, 4807, 2761, 679, 792, 675, 1916, 4687, 32, 50, 3314, 3559]), N);
m = 4, girth 12.
N = 571; P = mod( kron([0, 1, 461, 109]', [0, 1, 17, 184, 482]), N);
N = 1087; P = mod( kron([0, 1, 829, 257]', [0, 1, 4, 142, 1018, 1055]), N);
N = 2203; P = mod( kron([0, 1, 1917, 285]', [0, 1, 4, 130, 443, 1082, 1397]), N);
N = 4489; P = mod( kron([0, 1, 3789, 699]', [0, 1, 942, 1062, 1547, 2202, 1312, 3692]), N);
N = 8966; P = mod( kron([0, 1, 3977, 505]', [0, 1, 4987, 6942, 11, 17, 1158, 2049, 3754]), N);
m = 5, girth 10.
N = 511; P = mod( kron([0, 1, 265, 218, 27]', [0, 1, 3, 114, 244, 354]), N);
N = 763; P = mod( kron([0, 1, 251, 435, 76]', [0, 1, 3, 72, 81, 117, 720]), N);
N = 1067; P = mod( kron([0, 1, 604, 969, 560]', [0, 1, 3, 8, 32, 46, 812, 1050]), N);
N = 1417; P = mod( kron([0, 1, 142, 326, 948]', [0, 1, 3, 225, 386, 912, 972, 1294, 1337]), N);
N = 1991; P = mod( kron([0, 1, 1286, 1266, 1429]', [0, 1, 69, 226, 956, 469, 86, 316, 1344, 1643]), N);
N = 2873; P = mod( kron([0, 1, 577, 2534, 2634]',[ 0, 288, 303, 5, 904, 971, 1398, 1659, 1711, 2474, 2557]), N);
N = 4777; P = mod( kron([0, 1, 509, 1123, 3144]', [0, 1, 236, 3274, 274, 2549, 4372, 230, 41, 1612, 3429, 3540]), N);
N = 5649; P = mod( kron([0, 1, 1427, 2689, 1532]', [0, 713, 443, 455, 52, 1791, 193, 1939, 2166, 2665, 4505, 4969, 5520]), N);
N = 7199; P = mod( kron([0, 1, 1540]', [0, 325, 1083, 456, 4, 7, 29, 1672, 2984, 3879, 4733, 5276, 6337, 6974]), N);
m = 6, girth 8.
N = 101; P = mod( kron([0, 1, 36, 84, 95, 87]', [0, 1, 2, 3, 4, 26, 79]), N);
N = 121; P = mod( kron([0, 1, 3, 9, 27, 81]', [0, 1, 2, 7, 12, 24, 64, 116]), N);
N = 151; P = mod( kron([0, 1, 8, 64, 59, 19]', [0, 1, 2, 3, 4, 5, 6, 49, 108]), N);
N = 181; P = mod( kron([0, 1, 42, 135, 59, 125]', [0, 1, 2, 3, 10, 11, 21, 25, 101, 173]), N);
N = 181; P = mod( kron([0, 1, 42, 135, 59, 125]', [0, 1, 2, 3, 10, 35, 41, 51, 77, 132, 173]), N);
N = 181; P = mod( kron([0, 1, 42, 135, 59, 125]', [0, 1, 3, 10, 35, 38, 52, 86, 89, 105, 147, 156]), N);
N = 241; P = mod( kron([0, 1, 87, 98, 91, 205]', [0, 1, 2, 4, 5, 16, 31, 104, 106, 125, 175, 208, 212]), N);
N = 281; P = mod( kron([0, 1, 86, 90, 153, 232]', [ 0, 1, 18, 116, 173, 149, 13, 14, 117, 122, 146, 178, 179, 277]), N);
N = 331; P = mod( kron([0, 1, 64, 124, 323, 150]', [0, 1, 116, 216, 2, 100, 201, 20, 34, 61, 88, 108, 123, 158, 186]), N);
N = 401; P = mod( kron([0, 1, 39, 318, 372, 72]', [0, 1, 111, 112, 113, 292, 333, 98, 2, 108, 179, 261, 291, 305, 377, 382]), N);
N = 401; P = mod( kron([0, 1, 39, 318, 372, 72]', [0, 1, 111, 112, 113, 65, 51, 15, 31, 27, 36, 54, 58, 76, 90, 105, 145]), N);
N = 451; P = mod( kron([0, 1, 16, 256, 37, 141]', [0, 1, 157, 158, 159, 292, 314, 117, 207, 330, 9, 263, 109, 133, 152, 192, 255, 401]), N);
N = 521; P = mod( kron([0, 1, 25, 104, 516, 396]', [0, 1, 99, 100, 101, 2, 201, 421, 298, 234, 320, 196, 297, 299, 409, 434, 462, 470, 475]), N);
N = 571; P = mod( kron([0, 1, 106, 387, 481, 167]', [0, 1, 273, 274, 275, 296, 252, 317, 570, 299, 262, 547, 37, 103, 205, 225, 349, 368, 424, 509]), N);
N = 601; P = mod( kron([0, 1, 32, 423, 314, 432]', [0, 1, 136, 137, 138, 463, 412, 50, 596, 238, 589, 325, 279, 27, 69, 144, 488, 495, 502, 531, 600]), N);
N = 661; P = mod( kron([0, 1, 197, 471, 247, 406]', [0, 1, 57, 605, 58, 59, 603, 117, 176, 24, 251, 113, 331, 56, 10, 82, 152, 360, 412, 474, 565, 590]), N);
N = 751; P = mod( kron([0, 1, 80, 392, 569, 460]', [0, 1, 210, 211, 212, 420, 750, 542, 629, 579, 621, 124, 355, 342, 550, 11, 45, 51, 318, 407, 421, 551, 612]), N);
N = 781; P = mod( kron([0, 1, 5, 25, 125, 625]', [0, 1, 150, 151, 300, 2, 483, 152, 598, 630, 223, 235, 364, 210, 517, 502, 29, 154, 216, 255, 268, 358, 369, 379]), N);
N = 881; P = mod( kron([0, 1, 268, 463, 744, 286]', [0, 1, 326, 327, 328, 555, 556, 554, 226, 656, 2, 204, 430, 657, 363, 548, 537, 106, 319, 366, 391, 416, 645, 678, 735]), N);
N = 941; P = mod( kron([0, 1, 349, 412, 756, 364]', [0, 1, 227, 228, 229, 714, 713, 715, 453, 457, 940, 488, 419, 712, 255, 484, 202, 684, 40, 59, 80, 347, 466, 491, 531, 847]), N);
N = 941; P = mod( kron([0, 1, 349, 412, 756, 364]', [0, 1, 227, 228, 229, 714, 713, 715, 453, 457, 940, 260, 712, 484, 3, 53, 202, 381, 460, 96, 243, 321, 340, 419, 630, 644, 707]), N);
N = 1051; P = mod( kron([0, 1, 307, 710, 413, 671]', [0, 1, 72, 73, 74, 979, 977, 981, 251, 887, 655, 116, 248, 218, 134, 447, 371, 770, 3, 222, 75, 114, 136, 493, 614, 696, 737, 985]), N);
N = 1151; P = mod( kron([0, 1, 224, 683, 1060, 334]', [0, 1, 558, 559, 560, 593, 594, 592, 32, 1120, 36, 1066, 476, 1003, 303, 275, 149, 607, 48, 190, 360, 270, 538, 767, 853, 874, 877, 911, 993]), N);
N = 1151; P = mod( kron([0, 1, 224, 683, 1060, 334]', [0, 1, 558, 559, 560, 593, 594, 37, 591, 595, 2, 1116, 527, 562, 704, 679, 984, 466, 102, 220, 229, 298, 486, 537, 636, 700, 751, 954, 1016, 1080]), N);
m = 6, girth 10.
N = 971; P = mod( kron([0, 1, 803, 65, 732, 341]', [0, 1, 6, 585, 608, 725, 872]), N);
N = 1331; P = mod( kron([0, 1, 1170, 632, 735, 124]', [0, 1, 8, 45, 145, 674, 970, 1292]), N);
N = 1991; P = mod( kron([0, 1, 42, 1764, 421, 1754]', [0, 1, 9, 201, 28, 484, 775, 863, 927]), N);
N = 2801; P = mod( kron([0, 1, 7, 49, 343, 2401]', [0, 1, 302, 2628, 2109, 162, 338, 772, 1929, 2646]), N);
N = 3821; P = mod( kron([0, 1, 925, 3542, 1753, 1421]', [0, 1, 611, 3591, 1732, 36, 749, 1854, 2281, 2653, 3054]), N);
N = 4931; P = mod( kron([0, 1, 15, 225, 3375, 1315]', [0, 1, 212, 116, 451, 8, 638, 1515, 2391, 2676, 3444, 3978]), N);
N = 5801; P = mod( kron([0, 1, 3280, 3346, 5189, 5587]', [0, 1, 68, 2741, 4805, 4021, 2464, 2624, 3034, 3270, 3784, 4959, 5617]), N);
N = 7381; P = mod( kron([0, 1, 9, 81, 729, 6561]', [0, 61, 80, 881, 234, 59, 1987, 776, 2272, 2678, 3098, 4623, 6962, 7233]), N);

General articles on LDPC architecture, Usefull links
Survey articles on LDPC architecture
- E. Boutillon, C. Douillard, G. Montorsi, " Iterative Decoding of Concatenated Convolutional Codes: Implementation Issues", Proceedings of the IEEE, vol. 95, n°6, june 2007.
- "Codes et Turbocodes", Collection IRIS, C. Berrou (Réd.), Springer, Paris, 2007, 397 p. (Iris),
ISBN 978-2-287-32739-1
- COCA Project ; Channel coding: State of the art and perspectives", Internal Report, Groupe des Ecoles de Telecommunications (GET).
- WEB site of the TU Kaiserslautern that gives some ML decoding performance of several codes:
Maximum Likelihood (ML) Simulation Results
Hardware simulation of LDPC architecture: you can find information about the White Gaussian Noise Generator for channel emulation here ). You can also find a presentation of the implementation of this hardware for DVB-S2 emulation here ).

Return to
main page of Emmanuel Boutillon
Return to the main page of the lab
Return to the main page of the
university








.jpg)





